Ivan Lakhturov

Haskell allows to decompose arguments straight in a function signature. While pattern matching is implemented in some Scheme-s, it's not applied to the signature. Luckily, we have Scheme macros to alter that.

Let's say we started out with a new language, bootstrapping it with Scheme. And in the beginning we have no lexing / parsing, just redefinitions. First of all, we change the names for the pairs, as that's the cornerstone of Scheme and some other functional languages.

Why not to change those, indeed? Say, what is the meaning of 'cdr'? Perhaps, earlier "Contents of the Decrement part of Register number" meant something. But nowadays - nothing. The only advantage perhaps is that you can quickly write some 'cadadr'-like compositions.

So, we redefine pairs' functions:

Then, suppose we want to write a swap function, which interchanges the former and the latter parts of a pair:

Now compare this to the Haskell version:

Haskell decomposes a pair into "a" and "b" straight in the function signature. One can argue that it looses "p" variable name for the whole pair. But for that it has a special syntax:

Notice, we could not use the "pair" identifier in Scheme version, as we would shadow the constructor.

The Haskell's variant is more declarative. Also, if the variable "p" would have a longer name, we'd suffer, as it's used twice. Let's make use of macros to implement Haskell-like function definitions in Scheme:

The second transformer is to allow identifier definitions like "(≝ x 10)". The "match" is defined in PLT/Racket and some other implementations. Now we can write our swap-function like this:

or even like this:

- if we remember about the dot-notation of the Scheme's lexer (reader).

However, that will not work. The reason is simple, the redefinitions that we wrote for the pair funcions are executed in the last phase (run-time), but the "match" macro needs it already during the macro-application phase (the expander phase). That "match" does not know about new pair's constructor.

And to mitigate that there is a clumsy "define-match-expander":

The first transformer is used in the "match" context, and the second is for everything else (i.e. it replaces our "cons" pair constructor). The transformers are identical, but I didn't manage to declare one separately and re-use. Quick search reveals that others also have some problems with that.

So, now we can imitate Haskell notation. For one parameter and one pattern only, but that could be extended. Haskell, however, also has a limit of one pattern, as to declare a different pattern one needs to repeat a function name on a different line. That's what I don't like in Haskell. It is really enough to write a function name once. Say, in Nemerle with indentation-based syntax one can write:

There are case expressions in Haskell, but those oblige to declare additional identifiers for function's arguments (those could be replaced with _ in Nemerle). And hey! The "case" from Haskell resembles define/match, which is already implemented in PLT Scheme/Racket. And define/match is a good enough substitute for the default Haskell notation, I think. So, instead of "(define (swap p) (pair (latter p) (former p)))" we would write:

A bit too many parentheses to support multiple patterns for one branch (different from normal "match"), but in other respects nice.

So, actually I would choose Haskell-like notation for functions with one pattern, and define/match for many-pattern functions, like Fibonacci one. I guess it's possible to combine these in one ≝-notation. For that we would need to enhance the ≝ macro. But that is already "a topic of the future research", as scientists say (when they don't want (or cannot) continue).

Recently I've finished the website called Choose Your Textbook. This is a Scientific Literature Browser. One can browse there through the tree of science (the branches are taken from the wiki), and see the short description of those sciences. To the right there is an Amazon search box, where the name of the currently chosen branch is dynamically loaded, thus it shows the (most) relevant books at Amazon for a specific discipline.

Technically speaking, this is a mashup, but part of mashing is done offline. It's with my tools written in Scheme, and it is possible to do that dynamically, as there exist Scheme-s embedded to JS. But not for this project. The tooling converts that specific wiki-page in a chain HTML -> SXML -> (filtering) -> JSON. The latter is embedded to the website's JS. A nice tree / graph renderer called JIT is used to show the tree. JIT does animation / morphing and supports a few layouts. Seems, though, it cannot switch between them dynamically. I've stumbled at some other restrictions also, e.g. couldn't setup decent automatic node sizes.

Despite I've designed the website as an Amazon affiliate, I knew there wouldn't be much popularity. I tried to put a link to Hacker News and to Reddit, but both unsuccessful. So, there are almost no visitors at all. Nevertheless, my point was to try a few things: make my first mashup, write some tooling in Scheme, including DOM-manipulation, try out some web graph renderer, and last but not least, I wanted to skim through the tree of Science looking with one eye on existing appropriate literature list. And those goals are accomplished.

Let's first sing a beer song (in R6RS Scheme):

Then let's make an extra library:

... and we are ready to write yet-another HQ9+ interpreter:

HQ9+ is a joke language, featuring "Hello world" command, quine command, beer-song command and a counter increment (counter cannot be accessed or printed out). Quine implementation here is the classical "quine-cheating", where a program has access to its source. To make the quine more 'honest' somebody designed H9+. This is the same as HQ9+, but without "Q" command, and additionally, all characters on input are ignored, except for H, 9 and +. Then, obviously, "Hello, World!" program will be a quine. Let's implement H9+:

And let's implement also a variation of this theme, the esoterical language KL:

The semantics is as following: + is printing "Hello, world!" in Russian, - is printing a program's source, / is making a newline, and * print outs a poem from Russian movie "Brother".

To complete the picture, we can mention other close related to HQ9+ joke languages: HQ9++, CHIQRSX9, HQ9+B, HQ9+2D. HQ9++ is 'an object-oriented extension of HQ9+'; not interesting. CHIQRSX9+ adds eval, ROT-13 and sorting of input lines. ROT-13 (Caesar cipher) is a nice exercise to implement, but let's leave it for later. HQ9+B adds Brainfuck: this is definitely a thing to implement, but I will deal with Brainfuck later. HQ9+2D is not properly specified (even for a joke language), but commands it adds remind me 2D Turing-machine, so called Langton's ant. I want to implement and play with different Turing-machines, but later.

Later I will also look through the list of joke languages. For example, the first there is a 'language' 99, which just prints out '99 bottles of beer' song. Anyways, I hope, there could be something exciting in the list.

More than five years ago I worked for "DX-Complexes" and "Spectromed-UA". Here is a video about one of the projects I accomplished there. This is the aerodynamic calibration rig for metrological testing of spirographs. (What is a spirograph? See spirometry topic at Wikipedia).

http://www.youtube.com/watch?v=y4KBf_SQJhk

There is no sound in this video, cause we wanted to make a promo-video out of this, and some voiceover was supposed to be done later. But the device was too specialized, so we decided not to. So, let it be an advertisement for myself.

The schematics is in the illustration:

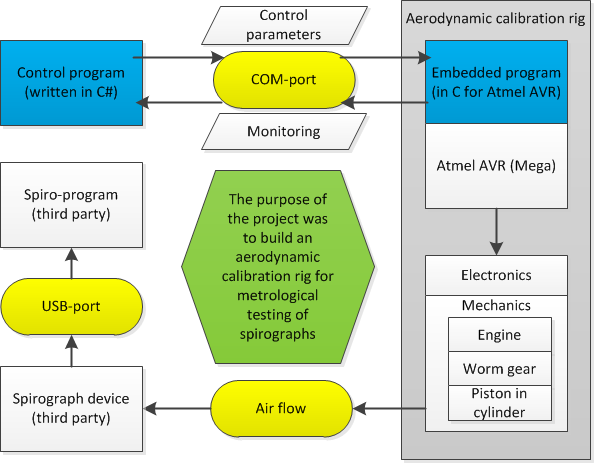
I operate the control program, written in C#, which communicates by COM-port with the embedded program in C. Both are written by me. Then this embedded program drives the device you see on video. It consists of electronics, the engine, worm gear and a piston going forwards and backwards in a plexiglass cylinder. The air flow generated by the device is registered with a spyrograph, connected via USB-port to another PC, where a third-party spirometry program is installed (visible in the second part of video).

Naturally, to verify the accuracy of a spiro-device, the calibration rig has to be in sctrict accuracy limits itself. It wasn't so trivial to achieve those specs. I remember one of the problems with overjumps: when you turn off the power of an engine, the piston doesn't stop momentarily due to inertia and slips further. What's the solution? To apply maximal reverse force via the engine as soon as the piston is supposed to stop. A period of time when we apply that reverse force depends on a few hard-to-estimate factors, so it was easier to fit this empirically.

This device can be considered as a very simple 'robot' with just one degree of freedom. Despite simplicity, it took us (2 people, me for software and a colleague for electronics and mechanics) around half a year of occasional work to get it done. Nevertheless, my friends in Ukraine report this device is still in field, they use it up to now without any complaints rising.

Find the largest palindrome made from the product of two 3-digit numbers.

And the last scratch for now. It is possible to prove that 11 divides a palindromic number. Indeed,

The factor 11 can belong to a - and in this case we step just 1 in b. But if 11 doesn't divide a, then we can increase b by 11 each time.

This speeds up the previous result around ten times, leaving an asymptotic behavior the same. The memory use is the same O(1).

Let's look at results:
k = 2 => N = 9009
k = 3 => N = 906609
k = 4 => N = 99000099
k = 5 => N = 9966006699
k = 6 => N = 999000000999
k = 7 => N = 99956644665999
k = 8 => N = 9999000000009999
...
We could improve our algo drastically, if proven that the sought-for palindrome is less or equal (and mirrored). I have the feeling that for even k it is equal. But I don't know how to prove it. (I calculated for k = 10 and this does not hold, N = 99999834000043899999).

Find the largest palindrome made from the product of two 3-digit numbers.

An author, however, advises a simpler approach. As we are looking for a palindrome a*b, let's iterate a and b in a top-down direction. After finding some palindrome, impose it as a top boundary for palindromes, that is, iterating in the inner loop for b, we stop when a*b cannot be large than that anymore. If we found a new palindrome, it will replace the boundary. Stop condition is finishing the outer loop in a, i.e. when it drops to 2-digits number (k-1, generally speaking).

Complexity in memory now is just O(1). Performance complexity by my impression is better than in the previous variant. The outer loop has n - n/10 steps, so it cannot be less than O(n). Assuming that a desired palindrome (left half of it, actually) lies close to (which should be proved, strictly speaking), we make no more than operations until find it, and no more than the same afterwards.

This is the worst case, however, and I hope that we find some worse-than-ideal palindrome quick enough. Suppose, we can use the estimate ab origin, i.e. the inequality holds, where f = n - a, g = n - b. Then we can calculate an estimate of operations as area under a curve y = n / x:

Find the largest palindrome made from the product of two 3-digit numbers.

Last time we had a straightforward algo with complexity and at least O(n) memory use. Now let's enhance that. Instead of iterating over multipliers it's reasonable to iterate over palindromes, starting from the largest. I.e. over sequence 999999, 998899, 997799, and so on.

Remark. The largest product of two 3-digit numbers is 999 * 999 = 998001. So, in principle, we could start from the palindrome 997799. But this saves just 2 iterations.

Having a palindrome m, we factorize it and look at all the subsets of the factorization. Assume, we have one subset already. Let's name the product of those factors as p. If this number p has k digits (k = 3 for now) and the number m/p has k digits, than we found the palindrome, which is a product of two k-digit numbers.

In Scheme that will be written as:

Here I used a few new util functions:

which make numbers out of their base-k representation.

Complexity now is hard to calculate. The worst case scenario gives quite a bad upper boundary. However, the worst case will never be realized.

Looking at what it gives out (9009, 906609, 99000099, 9966006699, 999000000999, ...), I could guess that the required palindrome is found after roughly iterations. So, in total I hope for less than complexity.

The memory use depends on factorizations - we store one whenever a palindrome is taken and lose it when proceed with the next palindrome.

Some years ago I accomplished a project of the real-time ECG-generator (the text is in Russian) for Spectromed-UA. I wrote a soft part in Delphi, and another guy dealt with an electronics part.

The device is connected to PC and sends out a signal via LPT to a DAC outside. A signal could be rectangular (meander), sinusoidal and ECG-like. (ECG is the electrocardiogram by the way). The 'heartbeat' of the latest one can be modulated in time. A subprogram to play out real ECG was included. Some noise modulation was included as well.

That was designed to test cardio-analyzers and similar devices. Small and neat project, as I remember. There was no support for the most pathological arrhythmias, however.

Opera 10 beta hits portages with its customizable speed dial feature. As for me, that could be better.

Why not to customize the grid of speed dial in such a way that a user can choose independently x-y size, with discretization 1 column-row? With my usual portrait display mode all the cells are concentrated in the center of a screen.

Something has to be done with shortcuts Ctrl+digit. Nine shortcuts are not enough for 25 cells anymore. I think that could be something like Ctrl+0, [switched to speed dial mode], digit, digit [i.e. up to 99 choices].

A hundred of those tabs should be ok, as for me.

I filed this bugreport them (reference email DSK-258394 at bugs.opera.com).

As I already posted in Scheme, a function computing all subsets of a set would be:

The same in Haskell:

For imperative languages I'd rather prefer bitwise approach. Here is in C#: